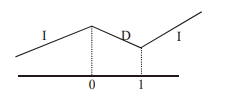
Q. Let $f(x)$ be a cubic polynomial on $R$ which increases in the interval $(-\infty, 0) \cup(1, \infty)$ and decreases in the interval $(0,1)$. If $f^{\prime}(2)=6$ and $f(2)=2$, then the value of $\tan ^{-1}( f (1))+\tan ^{-1}\left( f \left(\frac{3}{2}\right)\right)+\tan ^{-1}( f (0))$ cquals
Application of Derivatives
Solution:
$f^{\prime}(x)=k x(x-1)$
$f ^{\prime}(2)=2 k =6 \therefore k =3 $
$\therefore f ^{\prime}( x )=3 x ^2-3 x \Rightarrow f ( x )= x ^3-\frac{3 x ^2}{2}+ C$
$f (2)=8-6+ C =2+ C =2 \therefore C =0$
$\Rightarrow f ( x )= x ^2\left( x -\frac{3}{2}\right) .$