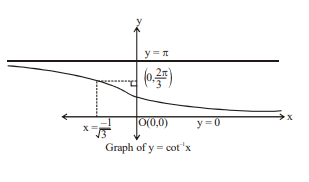
Question

Let $f: R \rightarrow\left(0, \frac{2 \pi}{3}\right]$ defined as $f(x)=\cot ^{-1}\left(x^2-4 x+\alpha\right)$. Find the smallest integral value of $\alpha$ such that $f ( x )$ is into function.

Answer 1

Clearly $x ^2-4 x +\alpha>$ or $\geq \frac{-1}{\sqrt{3}} \forall x \in R$
$\Rightarrow x ^2-4 x +\alpha+\frac{1}{\sqrt{3}}>0 \forall x \in R $
$\text { So, Discriment }<0 \Rightarrow 16-4\left(\alpha+\frac{1}{\sqrt{3}}\right)<0 $
$ 4-\alpha-\frac{1}{\sqrt{3}}<0 \Rightarrow \alpha>4-\frac{1}{\sqrt{3}} $
$\therefore \alpha \in\left(4-\frac{1}{\sqrt{3}}, \infty\right)$
$\text { Hence minimum integral } \alpha=4 $