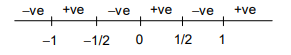Question

Let $f : IR \rightarrow IR$ be defined as $f ( x )=|x|+\left|x^{2}-1\right| .$ The total number of points at which $f$ attains either a local maximum or a local minimum is

Answer 1

$f'(x)=\frac{|x|}{x}+\frac{\left|x^{2}-1\right|}{x^{2}-1} \cdot(2 x)$
$ =
\begin{cases}
2x - 1, & x < -1 \\
-(2x + 1), &-1 < x < 0 \\
1-2x, & 0 < x < 1 \\
2x + 1 & x > 1
\end{cases} $

So, $f'(x)$ changes sign at points
$x=-1,-\frac{1}{2}, 0, \frac{1}{2}, 1$
so, total number of points of local maximum or minimum is $5 .$