Question

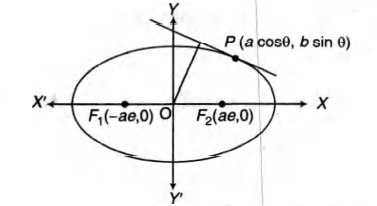
Let $d$ be the perpendicular distance from the centre of the ellipse $x^{2} / a^{2}+y^{2} / b^{2}=1$ to the tangent drawn at a point $P$ on the ellipse. If $F_{1}$ and $F_{2}$ are the two foci of the ellipsë, then show that
$\left(P F_{1}-P F_{2}\right)^{2}=4 a^{2}\left(1-\frac{b^{2}}{d^{2}}\right)$

Answer 1

Let the coordinates of point $P$ be $(a \cos \theta, b \sin \theta)$.
Then, equation of tangent at $P$ is
$\frac{x}{a} \cos \theta+\frac{y}{b} \sin \theta=1 ....$(i)
We have, $d=$ length of perpendicular from $O$ to the tangent at $P$

$d=\frac{|0+0-1|}{\sqrt{\frac{\cos ^{2} \theta}{a^{2}}+\frac{\sin ^{2} \theta}{b^{2}}}} \Rightarrow \frac{1}{d}=\sqrt{\frac{\cos ^{2} \theta}{a^{2}}+\frac{\sin ^{2} \theta}{b^{2}}} $
$\Rightarrow \frac{1}{d^{2}}=\frac{\cos ^{2} \theta}{a^{2}}+\frac{\sin ^{2} \theta}{b^{2}}$
We have to prove $\left(P F_{1}-P F_{2}\right)^{2}=4 a^{2}\left(1-\frac{b^{2}}{d^{2}}\right)$
Now, $RHS =4 a^{2}\left(1-\frac{b^{2}}{d^{2}}\right) $
$=4 a^{2}-\frac{4 a^{2} b^{2}}{d^{2}}$
$=4 a^{2}-4 a^{2} b^{2}\left(\frac{\cos ^{2} \theta}{a^{2}}+\frac{\sin ^{2} \theta}{b^{2}}\right) $
$=4 a^{2}-4 b^{2} \cos ^{2} \theta-4 a^{2} \sin ^{2} \theta$
$=4 a^{2}\left(1-\sin ^{2} \theta\right)-4 b^{2} \cos ^{2} \theta$
$=4 a^{2} \cos ^{2} \theta-4 b^{2} \cos ^{2} \theta$
$=4 \cos ^{2} \theta\left(a^{2}-b^{2}\right)=4 \cos ^{2} \theta \cdot a^{2} e^{2}\left[\because e=\sqrt{1-(b / a)^{2}}\right]$
Again, $P F_{1}=e|a \cos \theta+a| e \mid$
$=a|e \cos \theta+1|$
$=a(e \cos \theta+1)$
$[\because-1 \leq \cos \theta \leq 1$ and $0 Similarly, $ P F_{2}=a(1-e \cos \theta)$
Therefore, LHS $=\left(P F_{1}-P F_{2}\right)^{2}$
$=[a(e \cos \theta+1)-a(1-e \cos \theta)]^{2}$
$=(a e \cos \theta+a-a+a e \cos \theta)^{2}$
$=(2 a e \cos \theta)^{2}=4 a^{2} e^{2} \cos ^{2} \theta$
Hence, LHS $=$ RHS