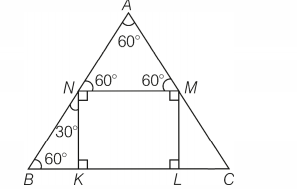
Question

Let $ABC$ be an equilateral triangle, let $KLMN$ be a rectangle with $K, L$ on $BC, M$ on $AC$ and $N$ on $AB$ Suppose $AN/NB =2$ and the area of $\Delta\,BKN$ is $6$ the area of the $\Delta\,ABC$ is

• A. 54
• B. 108
• C. 48
• D. not determinable with the above data

Answer 1

Answer: (B)

Given,

$ABC$ is an equilateral triangle
$\therefore AB= BC =AC$
$KLMN$ be a rectangle
$\therefore KL=MN$
and $NK=LM$
$\frac{AN}{NB}=2$
$\therefore AN=2NB=AM=MN$
$AB=AN+NB=3NB$
Area of $\Delta BKN=6$
In $\Delta\,BKN$,
$sin\,60^{\circ}=\frac{NK}{BN}$
$\Rightarrow NK= \frac{\sqrt{3}}{2}BN$
Area of $\Delta\,BKN=\frac{1}{2}\cdot BN \cdot NK\,sin\,30^{\circ}$
$\Rightarrow 6=\frac{1}{2}.BN.\frac{\sqrt{3}}{2}. BN. \frac{1}{2}$
$ \Rightarrow BN^{2}=\frac{48}{\sqrt{3}}$
$\therefore $ Area of $\Delta ABC=\frac{\sqrt{3}}{4}\times AB^{2}$
$=\frac{\sqrt{3}}{4}\times9BN^{2}=\frac{\sqrt{3}}{4}\times9\times\frac{48}{\sqrt{3}}=108$