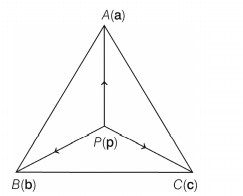
Question

Let $ABC$ be a triangle and $P$ be a point inside $ABC$ such that $\overrightarrow{PA}+2\,\overrightarrow{PB}+3\, \overrightarrow{PC}=0$ The ratio of the area of $\Delta\, ABC$ to that of $\Delta\,APC$ is

• A. $2$
• B. $\frac{3}{2}$
• C. $\frac{5}{3}$
• D. $3$

Answer 1

Answer: (D)

Given,
Point $P$ inside the $\Delta\, ABC$ such that
$PA+2PB+3PC=0$

Let $PA = a - P$
$PB=b-P$
$PC=c-P$
$\therefore (a-p)+2 (b-p)+3 (c-P)=0$
$\Rightarrow a+2b+3c=3P$
$\Rightarrow p=\frac{a+2b+3c}{6}$
Area of $\Delta APC =\frac{1}{2} | a \times P+P\times c +c \times a|$
$=\frac{1}{2}\left|a\times\frac{\left(a+2b+3c\right)}{6}+\frac{\left(a+2b+3c\right)}{6}\times c+c\times a\right|$
$=\frac{1}{2\times6}\left|2\left(a\times b\right)+3\left(a\times c\right)+\left(a\times c\right)+2\left(b\times c\right)+6 c\times a\right|$
$=\frac{1}{6} \left|a\times b+b\times c+c\times a\right|$
$\therefore \frac{\text{Area of $\Delta$ ABC}}{\text{Area of $\Delta$ APC}}=\frac{\frac{1}{2}\left|a\times b+b\times c+c\times a\right|}{\frac{1}{6}\left|a\times b+b\times c+c\times a\right|}=3 $
$\therefore $ Ratio $=3 : 1$