Q.
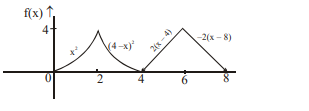
Let a function $f$ satisfying the relation $f(x+8)=f(x)$ and $f(x)=\begin{cases}x^2, & 0 \leq x \leq 2 \\ (4-x)^2, & 2< x \leq 4 \\ 2(x-4), & 4< x< 6 \\ -2(x-8), & 6 \leq x \leq 8\end{cases}$.
The value of $f(19) + f(63)+f(99) + f(-73)$ is equal to
Relations and Functions - Part 2
Solution: