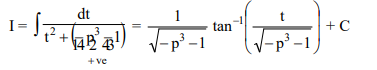Question

$\int \frac{\left(e^x+1\right) d x}{e^{2 x}+x^2+2 x e^x-p^3-1}$ is equal to
[Note: C is the constant of integration.]

• A. $\frac{1}{\sqrt{- p ^3-1}} \tan ^{-1}\left(\frac{ e ^{ x }+ x }{\sqrt{- p ^3-1}}\right)+ C$ for $p <-1$
• B. $\frac{1}{2 \sqrt{- p ^3-1}} \ln \left|\frac{ e ^{ x }+ x -\sqrt{- p ^3-1}}{ e ^{ x }+ x +\sqrt{- p ^3-1}}\right|+ C$ for $p <-1$
• C. $\frac{-1}{ e ^{ x }+ x }+ C$ for $p =-1$
• D. $\frac{1}{2 \sqrt{ p ^3+1}} \ln \left|\frac{ e ^{ x }+ x -\sqrt{ p ^3+1}}{ e ^{ x }+ x +\sqrt{ p ^3+1}}\right|+ C$ for $p >-1$

Answer 1

Answer: (A), (C), (D)

$ I=\int \frac{\left(e^x+1\right) d x}{\left(e^x+x\right)^2-p^3-1}$
put $e ^{ x }+ x = t \Rightarrow\left( e ^{ x }+1\right) dx = dt$
$I=\int \frac{d t}{t^2-p^3-1}$
(A) & (B) for $p <-1$

(C) for $p =-1$
$I =\frac{ dt }{ t ^2}=\frac{-1}{ t }+ C$
(D) for $p >-1$
$I=\int \frac{d t}{t^2-\left(p^3+1\right)}=\frac{1}{2 \sqrt{p^3+1}} \ln \left|\frac{t-\sqrt{p^3+1}}{t+\sqrt{p^3+1}}\right|+C$