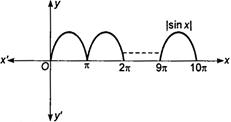
Question

$ \int\limits_{0}^{10\pi }{|\sin x|}\,\,dx $ is:

• A. 20
• B. 8
• C. 10
• D. 18

Answer 1

Answer: (A)

The period of $ |\sin x| $ is $ n $ .
$ \int\limits_{0}^{10\pi }{|\sin x|}\,\,dx $
$ =\left[ \int\limits_{0}^{\pi /2}{\sin x\,\,dx+\int\limits_{\pi /2}^{\pi }{\sin x}\,\,dx} \right] $
$ =10[-\cos x]_{0}^{\pi /2}+[-\cos x]_{\pi /2}^{\pi } $
Alternative Solution:
$ \therefore $ Required area $ =10\int\limits_{0}^{\pi }{\sin x}\,\,dx $
$ =10[-\cos x]_{0}^{\pi }=-10(\cos \pi -\cos 0)=20 $