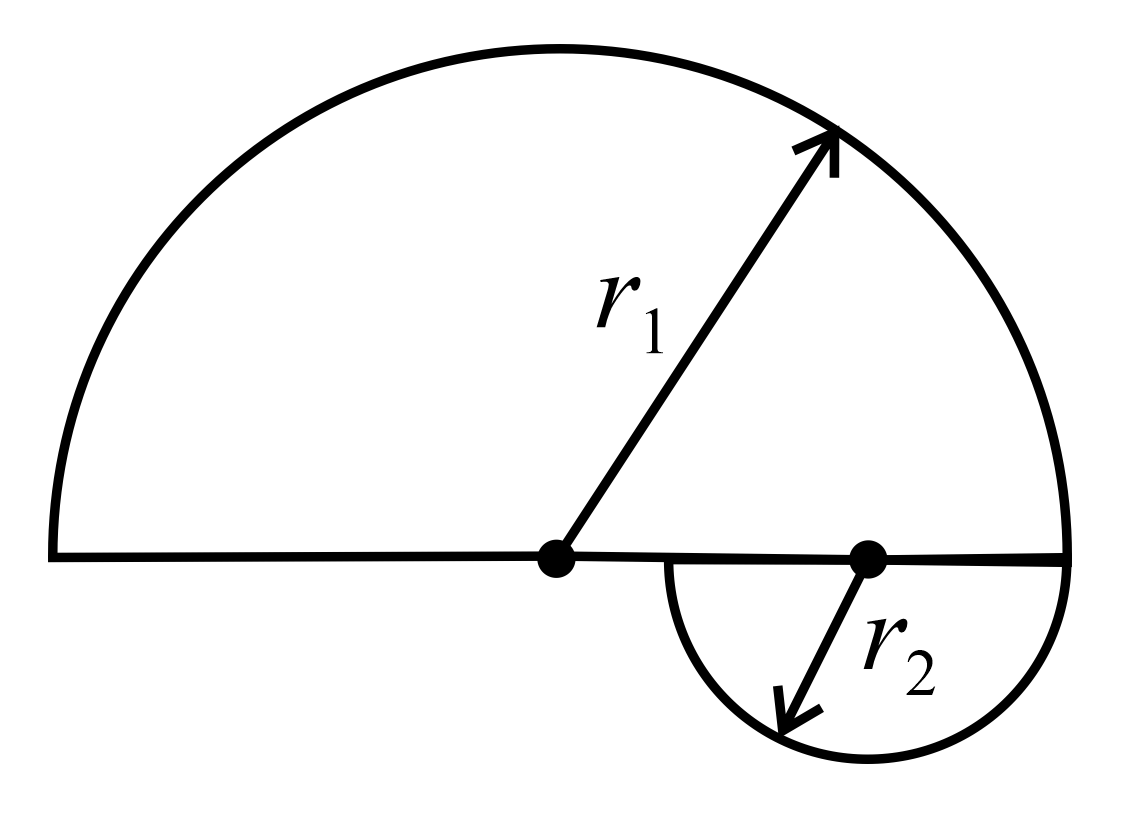Question

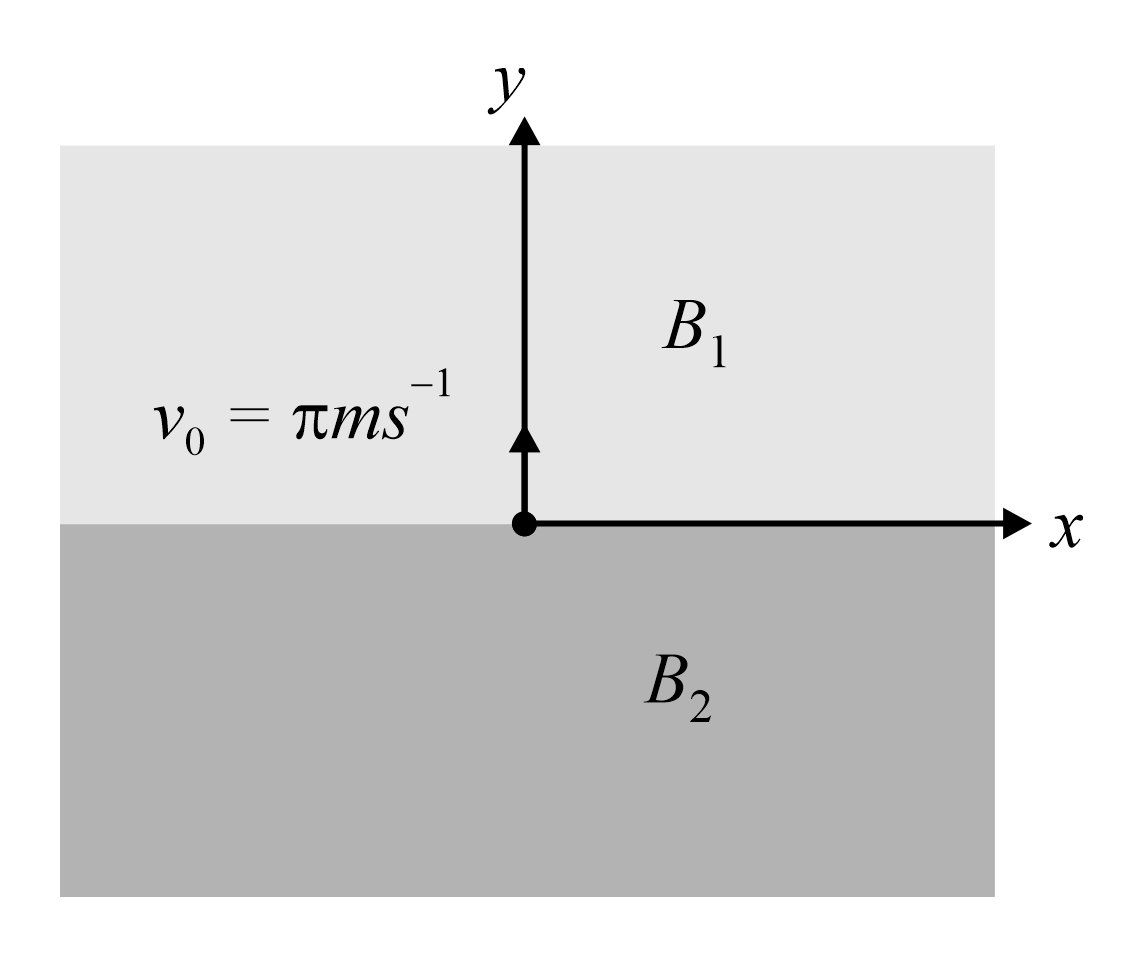
In the xy – plane, the region $y>0$ has a uniform magnetic field $B_{1}\hat{k}$ and the region $y < 0$ has another uniform magnetic field $B_{2}\hat{k}$ . A particle with a speed $v_{0}=\pi ms^{- 1}$ at $t = 0$ is projected in positive y-axis from the origin as shown in the figure. Neglect gravity in this problem. Let $t = T$ be the time when the particle crosses the x-axis from below for the first time. If $B_{2} = 4 B_{1}$ , the average speed of the particle, in $ms^{- 1}$ , along the x-axis in the time interval $T$ is ________.

Answer 1

$\left(\right.i\left.\right)$ Average speed along x - axis

$\left\langle V_{x}\right\rangle=\frac{\int\left|\overrightarrow{v_{x}}\right| d t}{\int d t}=\frac{d_{1}+d_{2}}{t_{1}+t_{2}}$
$\left(\right.ii\left.\right)$ We have,
$r_{1}=\frac{m v}{q B_{1}},r_{2}=\frac{m v}{q B_{2}}$
Since, $B_{1}=\frac{B_{2}}{4}$
$\therefore \, \, r_{1}=4r_{2}$
Time in $B_{1}\Rightarrow \frac{\pi m}{q B_{1}}=t_{1}$
Time in $B_{2}\Rightarrow \frac{\pi m}{q B_{2}}=t_{2}$
Total distance along x - axis $d_{1}+d_{2}=2r_{1}+2r_{2}=2\left(r_{1} + r_{2}\right)=2\left(5 r_{2}\right)$
Total time $T=t_{1}+t_{2}=5t_{2}$
$\therefore \, \, $ Average speed $=\frac{10 r_{2}}{5 t_{2}}=\frac{2 m v}{q B_{2}}\times \frac{q B_{2}}{\pi m}=2$