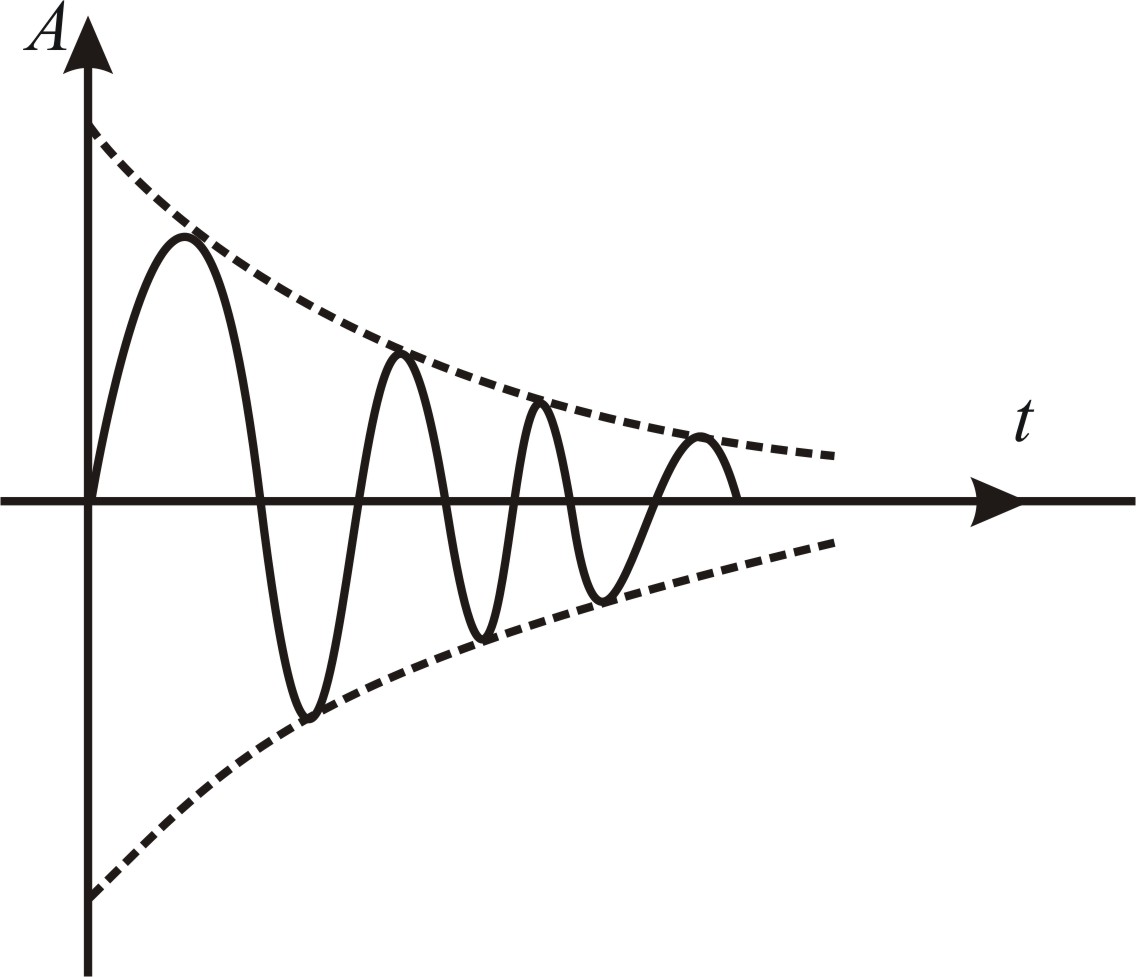
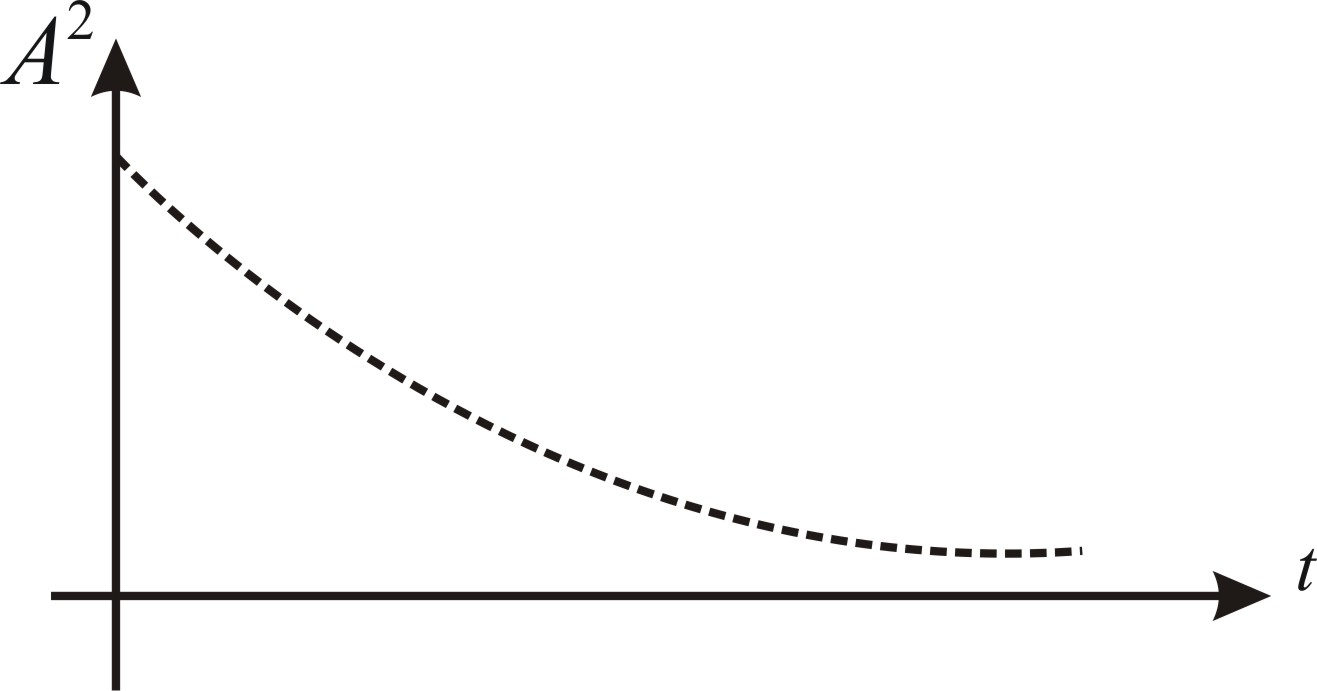
Q. In an Experiment to find the loss of energy with respect to time in case of swinging simple pendulum, the graph between square of amplitude and time is best represented by
NTA AbhyasNTA Abhyas 2020Oscillations
Solution: