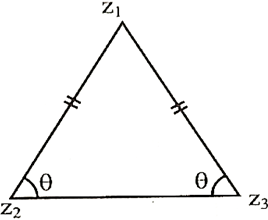
Question

If $z_{1}, \, z_{2}$ and $z_{3}$ are the vertices of a triangle in the argand plane such that $\left|z_{1} - z_{2}\right|=\left|z_{1} - z_{3}\right|,$ then $\left|arg \left(\frac{2 z_{1} - z_{2} - z_{3}}{z_{3} - z_{2}}\right)\right|$ is

• A. $\frac{\pi }{3}$
• B. $0$
• C. $\frac{\pi }{2}$
• D. $\frac{\pi }{6}$

Answer 1

Answer: (C)

$\frac{z_{1} - z_{2}}{z_{3} - z_{2}}=\frac{\left|z_{1} - z_{2}\right|}{\left|z_{3} - z_{2}\right|}e^{i \theta }\frac{z_{1} - z_{2}}{z_{2} - z_{3}}=\frac{\left|z_{1} - z_{3}\right|}{\left|z_{2} - z_{3}\right|}e^{- i \theta }$
$\Rightarrow \left(\frac{z_{1} - z_{2}}{z_{3} - z_{2}} + \frac{z_{1} - z_{3}}{z_{3} - z_{2}}\right)=$ purely imaginary number
$arg\left(\frac{2 z_{1} - z_{2} - z_{3}}{z_{3} - z_{2}}\right)=\pm\frac{\pi }{2}$