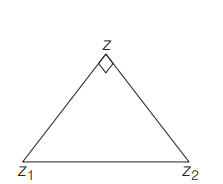Question

If $z_{1}=2-3 i$ and $z_{2}=-1+i$, then the locus of a point $P$ represented by $z=x+i y$ in the argand plane satisfying the equation $\arg \left(\frac{z-z_{1}}{z-z_{2}}\right)=\frac{\pi}{2}$ is

• A. $x^{2}+y^{2}-x+2 y-5=0$
• B. $x^{2}+y^{2}-x+2 y-5=0$ and $4 x+3 y+1<0$
• C. $4 x+3 y+1=0$ and $x^{2}+y^{2}-x+2 y-5>0$
• D. $x^{2}+y^{2}-x+2 y-5=0$ and $4 x+3 y+1>0$

Answer 1

Answer: (D)

We have,
$z_{1}=2-3 i, z_{2}=-1+i$
and $\arg \left(\frac{z-z_{1}}{z-z_{2}}\right)=\frac{\pi}{2}$
$\therefore \left|z-z_{1}\right|^{2}+\left| z_{2}-z_{2}\right|^{2}=\left| z_{1}-z_{2}\right|^{2}$
$\Rightarrow |z-(2-3 i)|^{2}+|z-(-1+i)|^{2}=|2-3 i+1-i|^{2}$
$\Rightarrow (x-2)^{2}+(y+3)^{2}+(x+1)^{2}+(y-1)^{2}=9+16$
$[\because z=x +i y]$
$\Rightarrow x^{2}-4 x+4+y^{2}+6 y+9+x^{2}+2 x+1+y^{2}$
$-2 y+1=25$
$\Rightarrow 2 x^{2}+2 y^{2}-2 x+4 y-10=0$
$\Rightarrow x^{2}+y^{2}-x+2 y-5=0$
Now equation of line paring through
$z_{1}(2,-3)$ and $z_{2}(-1,1)$ is
$y+3=\frac{1+3}{-1-2}(x-2)$
$\Rightarrow y+3=\frac{4}{-3}(x-2)$
$\Rightarrow -3 y-a=4 x-8$
$\Rightarrow -3 y-9=4 x-8$
$\Rightarrow 4 x+3 y+1=0$
According to given condition, $z$ should not lies on $z_{1}$ and $z_{2}$
$\therefore 4 x+3 y+1>0$