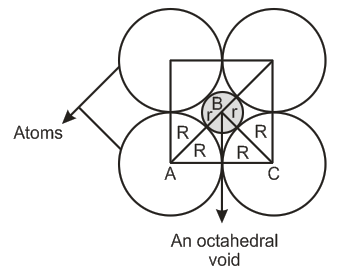
Question

If the radius of octahedral voids and radius of the atoms in close-packing are r and R, respectively. Derive the relation between r and R. What is the ratio of $100\times \frac{r}{R}.$ (Give answer to the nearest integer.)

Answer 1

Derivation of relation between r and R
A sphere fitted into the octahedral void is shown by shaded circle. The spheres present in other layers are not shown in the figure

∴ ΔABC is a right angled triangle.
∴ We apply pythagoras theorem.
AC² = AB² + BC²
(2R)² = (R + r) ² + (R + r)² = 2 (R + r)²
4R² = 2 (R + r)²
2 R² = (R + r)²
2 R² = (R + r)²
$\left(\sqrt{2} R \right)^{2} = \left( R ⁡ + r ⁡\right)^{2}$
$\sqrt{2} R = R ⁡ + r ⁡$
$ r = \sqrt{2} R ⁡ - R ⁡$
$ r = \left(\sqrt{2} - 1\right) R ⁡$
r = (1.414 – 1) R
r = 0.414 R
$\frac{100 r}{R}=41$