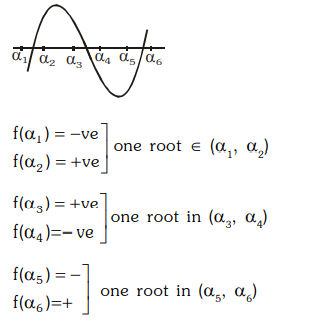Question

If $\alpha_1< \alpha_2< \alpha_3< \alpha_4< \alpha_5< \alpha_6$, then the equation $\left(x-\alpha_1\right)\left(x-\alpha_3\right)\left(x-\alpha_5\right)+3\left(x-\alpha_2\right)\left(x-\alpha_4\right)\left(x-\alpha_6\right)=0$ has -

• A. three real roots
• B. no real root in $\left(-\infty, \alpha_1\right)$
• C. one real root in $\left(\alpha_1, \alpha_2\right)$
• D. no real root in $\left(\alpha_5, \alpha_6\right)$

Answer 1

Answer: (A), (B), (C)

Correct answer is (a) three real rootsCorrect answer is (b) no real root in $\left(-\infty, \alpha_1\right)$Correct answer is (c) one real root in $\left(\alpha_1, \alpha_2\right)$