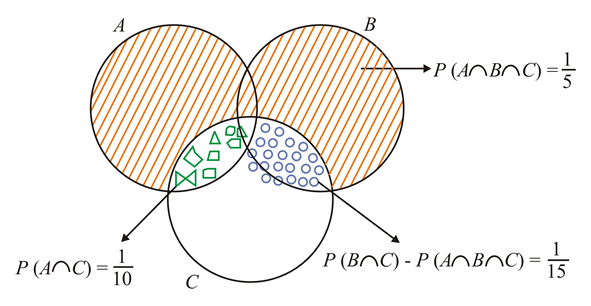
Question

If $A, \quad B$ and $C$ are exhaustive events satisfying $P((A \cup B) \cap C)=\frac{1}{5}$, $P(B \cap C)-P(A \cap B \cap C)=\frac{1}{15}$ and $P(A \cap C)=\frac{1}{10}$ then $P(C \cap(A \bar{\cup} B))$ is equal to

• A. $\frac{17}{30}$
• B. $\frac{18}{30}$
• C. $\frac{19}{30}$
• D. $\frac{20}{30}$

Answer 1

Answer: (C)

We have,
$P\left(\left(A \cup B\right) \cap \bar{C}\right)=\frac{1}{5}$
$P\left(B \cap C\right)-P\left(A \cap B \cap C\right)=\frac{1}{15}$
$P\left(A \cap C\right)=\frac{1}{10}$
$P(C \cap(A \cup \bar{U}))=?$
Now,

Then,
$P\left(C\right)+P\left(\left(A \cup B\right) \cap \bar{C}\right)=1$
$\Rightarrow P\left(C\right)=1-\frac{1}{5}=\frac{4}{5}$
And, $ \begin{array}{l} P(C \cap(A \cup \bar{B}))=P(C)-[P(B \cap C)-P(A \cap B \cap C)+P(A \cap C)] \\ \Rightarrow P(C \cap(A \bar{\cup} B))=\frac{4}{5}-\left(\frac{1}{15}+\frac{1}{10}\right)=\frac{19}{30} \end{array} $