Question

Hydrogen atom in ground state is excited by a monochromatic radiation of $\lambda = 975 \,\mathring{A}$. Number of spectral lines in the resulting spectrum emitted will be

• A. 3
• B. 2
• C. 6
• D. 10

Answer 1

Answer: (C)

Energy of the photon, $E=\frac{h c}{\lambda}$
$E=\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{975 \times 10^{-10}} J $
$=\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{975 \times 10^{-10} \times 1.6 \times 10^{-19}}\, eV =12.75 \,eV$
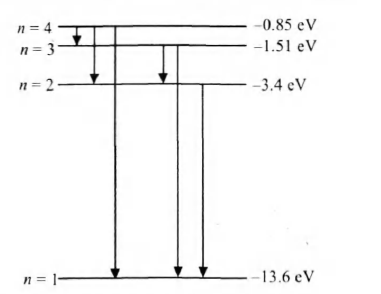
After absorbing a photon of energy $12.75 \,eV$, the electron will reach to third excited state of energy $-0.85 \,eV$,
since energy difference corresponding
to $n=1$ and $n=4$ is $12.75 \,eV$.
$\therefore$ Number of spectral lines emitted
$=\frac{(n)(n-1)}{2}=\frac{(4)(4-1)}{2}=6$