Q.
For a hypothetical reaction, $A_{(g)} +B_{(g)} \rightleftharpoons C_{(g)} +D_{(g)}$ a graph between $log\, K$ and $T^{-1}$ is straight line as follows, where $θ = tan^{-1}\, 0.5$ and $OA = 10$.
Assuming $ΔH^°$ is independent of temperature, the equilibrium constants at $298\, K$ and $798\, K$ are respectively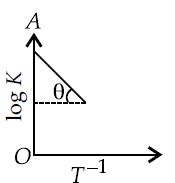
Equilibrium
Solution: