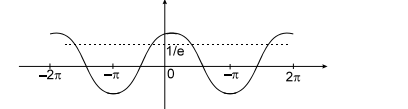
Question

$\cos (\alpha-\beta)=1$ and $\cos (\alpha+\beta)=\frac{1}{e}$, where $\alpha, \beta \in[-\pi, \pi]$. Number of pairs $(\alpha, \beta)$ which satisfy both the equations is/are

• A. 0
• B. 1
• C. 2
• D. 4

Answer 1

Answer: (D)

$\alpha-\beta=0,-2 \pi \text { or } 2 \pi$
$\alpha-\beta=0$
$\Rightarrow \alpha=\beta \Rightarrow \cos 2 \beta=\frac{1}{e}$
This is true for ' 4 ' values of ' $\alpha$ ', ' $\beta$ '
If $\alpha-\beta=-2 \pi \Rightarrow \alpha=-\pi$ and $\beta=\pi$ and $\cos (\alpha+\beta)=1 \Rightarrow$ (No solution)
similarly if $\alpha-\beta=2 \pi \Rightarrow \alpha=\pi$ and $\beta=-\pi$ again no solution results