Question

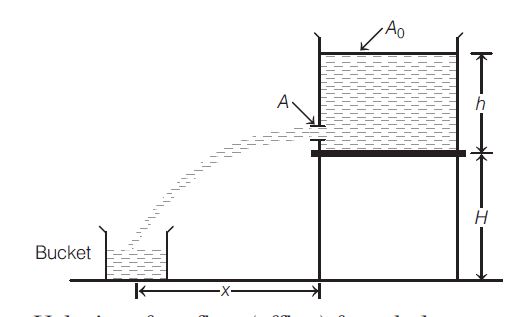
Consider the configuration of a stationary water tank of cross-section area $A_{0}$ and a small bucket as shown in figure below;

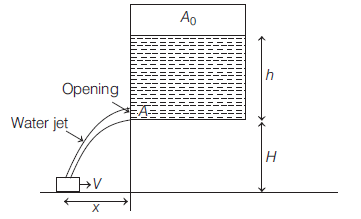
What should be the speed $v$ of the bucket, so that the water leaking out of a hole of cross-section area $A$ (as shown) from the water tank does not fall outside the bucket?
(Take, $h=5 \,m , H=5 \,m , g=10\, m / s ^{2}, A=5\, cm ^{2}$ and $\left.A_{0}=500\, cm ^{2}\right)$

• A. 1 m/s
• B. 0.5 m/s
• C. 0.1 m/s
• D. 0.05 m/s

Answer 1

Answer: (C)

Velocity of outflow (efflux) from hole
$=\sqrt{2gh.}$
Range of water jet,
$x=\sqrt{2gh}\times$ Time of fall
$=\sqrt{2gh} \times\sqrt{\frac{2H}{g}}=2\sqrt{hH}$
Velocity $v$ of bucket is
$\upsilon=\frac{dx}{dt}=\frac{d}{dt}2\sqrt{hH}$
$2\sqrt{H}.\frac{d\sqrt{h}}{dt}$
$\Rightarrow \upsilon=2\sqrt{H}.\frac{1}{2\sqrt{h}}.\frac{dh}{dt}$
$=\sqrt{\frac{H}{h}}.\frac{dh}{dt}\ldots\left(i\right)$
Now, using equation of continuity at area $A_{0}$ and area $A$ we have
$A\upsilon_{1}=A_{0}V$
where, $\upsilon_{1}=\sqrt{2gh}$
and $V=\frac{dh}{dt}.$
$\therefore A\sqrt{2gh}=A_{0}\left(\frac{dh}{dt}\right)$
Substituting for $\frac{dh}{dt}$ from Eq $\left(i\right),$ we get
$\upsilon=\sqrt{\frac{H}{h}}.\frac{A}{A}.\sqrt{2gh}$
$=\sqrt{\frac{5}{5}}.\left(\frac{5}{500}\right).\sqrt{2\times10 \times5}$
$=\frac{1}{10}ms^{-1}$
$=0.1\,ms^{-1}$