Q.
Consider the $bcc$ unit cells of the solids $1$ and $2$ with the position of atoms as shown below. The radius of atom $B$ is twice that of atom $A$. The unit cell edge length is $50\%$ more in solid $2$ than in $1$. What is the approximate packing efficiency in solid $2$ ?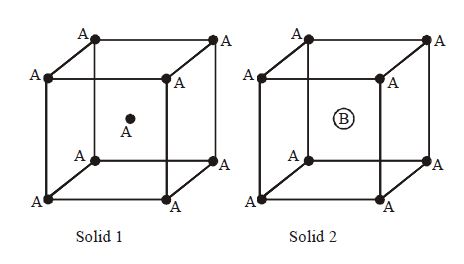
Solution: