Q.
Choose the correct options using the $V-T$ diagram
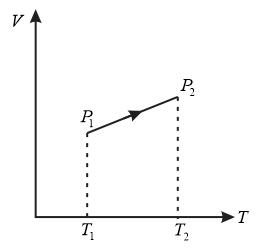
NTA AbhyasNTA Abhyas 2020
Solution:
Comparing the curve with equation of straight line
$y=mx+c$
we get
$V=aT+b$
where $a=$ slope,
$b=$ constant
we know that ideal gas equation of a gas is
$PV=nRT$
Putting the value of volume as the above equation
$P=\frac{n R T}{a T + b}=\frac{n R}{a + \frac{b}{T}}$
we know that $T_{2}>T_{1}$ (from the graph)
so $\frac{b}{T_{2}} < \frac{b}{T_{1}}$
we can conclude
$\therefore P_{2}>P_{1}$
$y=mx+c$
we get
$V=aT+b$
where $a=$ slope,
$b=$ constant
$PV=nRT$
Putting the value of volume as the above equation
$P=\frac{n R T}{a T + b}=\frac{n R}{a + \frac{b}{T}}$
so $\frac{b}{T_{2}} < \frac{b}{T_{1}}$
we can conclude
$\therefore P_{2}>P_{1}$