Question

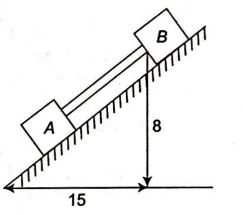
Blocks $A$ and $B$ in the figure are connected by a bar of negligible weight. Mass of each block is $170\, kg$ and $\mu_{A} = 0.2$ and $\mu_{B}=0.4$, where $\mu_{A}$ and $\mu_{B}$ are the coefficients of limiting friction between blocks and plane, calculate the force developed in the bar $(g= 10 \,m/sec^{2})$:

• A. $150\,N$
• B. $75\,N$
• C. $200\,N$
• D. $250\,N$

Answer 1

Answer: (A)

If the plane makes an angle $\theta$ with horizontal
$tan\,\theta=8/15$ If $R$ is the normal reaction
$R=170\,g\,cos\,\theta=170 \times 10 \times \left(\frac{15}{17}\right)$
$=1500\,N$
Force of friction on $A=1500 \times 0.2 =300\,N$
Force of friction on $B=1500 \times 0.4 =600\,N$
Considering the two blocks as a system, the net force parallel to the plane
$=2 \times 170\,g\,sin\,\theta-300-600$
$=1600-900=700\,N$
$\therefore $ Acceleration $=\frac{700}{340}=\frac{35}{17}m/s^{2}$
Consider the motion of A alone
$170\,g\,sin\,\theta-300-P=170 \times \frac{35}{17}$
(where P is pull on the bar)
$P=500-350$
$=150\,N$