Question

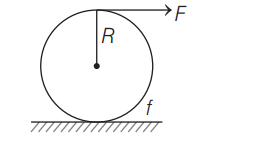
A tangential force $F$ acts at the top of a thin spherical shell of mass $m$ and radius $R$. The acceleration of the shell if it rolls without slipping is
$(f=$ rolling friction $)$

• A. $\frac{5 F}{6 m}$
• B. $\frac{6 F}{5 m}$
• C. $\frac{3 F}{2 m}$
• D. $\frac{F}{6 m}$

Answer 1

Answer: (B)

Torque due to the force $F$ on a thin spherical shell,
$\tau =r \times F$
$=2 R\, F \sin 90^{\circ}=2 R \,F\left[\because \sin 90^{\circ}=1\right]$
$\because$ Angular acceleration,
$\alpha=\frac{\tau}{I}\,\,\,....(i)$
Where, $I$ is moment of inertia of a thin spherical shell.
From parallel axes's theorem, moment of inertia of spherical shell,
$I=I_{ cm }+M r^{2}$
or $I=\frac{2}{3} M R^{2}+M R^{2} (\because r=R)$
From Eqs. (i), we get
$\alpha= \frac{2 R F}{\frac{2}{3} M R^{2}+M R^{2}} $
$ =\left(\frac{6}{5}\right) \frac{F}{R M}$
Hence, the tangential acceleration, $a_{T}=R \alpha$
Or $a_{T}=\left(\frac{6}{5}\right) \frac{F}{R M} \times R=\frac{6}{5} \frac{F}{M}$