Q.
A solid uniform cylinder of mass $m=6 \,kg$ and radius $r=0.1 \,m$ is kept in balance on a slope of inclination $\alpha=37^{\circ}$ with the help of a thread fastened to its jacket. The cylinder does not slip on the slope. The minimum required coefficient of friction to keep the cylinder in balance when the thread is held vertically is given as $\mu$. The value of $4 \mu$ is ___.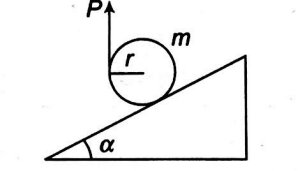
System of Particles and Rotational Motion
Solution: