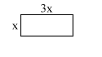
Question

A solid rectangular brick is to be made from 1 cu feet. of clay. The brick must be 3 times as long as it is wide. The ratio of height to width of the brick for which it will have minimum surface area, is

• A. $\frac{2}{9}$
• B. $\left(\frac{2}{9}\right)^{\frac{1}{3}}$
• C. $\frac{2}{3}$
• D. $\frac{3}{2}$

Answer 1

Answer: (D)

$3 x^2 h=1 $
$S=2\left(h x+3 x^2+3 x h\right) $
$S=2\left(3 x^2+4 h x\right)=2\left(3 x^2+4 x \cdot \frac{1}{3 x^2}\right) $
$S(x)=2\left(3 x^2+\frac{4}{3 x}\right) $
$S^{\prime}(x)=2\left(6 x+\frac{4}{3 x^2}\right)=0 ; x^3=\frac{2}{9}$
$\Rightarrow x=\left(\frac{2}{9}\right)^{\frac{1}{3}}$
now $ h =\frac{1}{3 x ^2} ; $ hence $\frac{ h }{ x }=\frac{1}{3 x ^2} \cdot \frac{1}{ x }=\frac{1}{3 x ^3}=\frac{1 \cdot 9}{3 \cdot 2}=\frac{3}{2}$