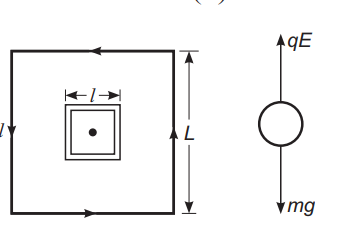
Question

A small square loop of wire of side $l$ is placed inside a large square loop of side $L(L>>l)$. If the loops are coplanar and their centres coincide, the mutual induction of the system is directly proportional to :

• A. $\frac{L}{l}$
• B. $\frac{l}{L}$
• C. $\frac{L^{2}}{l}$
• D. $\frac{l^{2}}{L}$

Answer 1

Answer: (D)

Considering the larger loop to be made up of four rods each of length $L$, the field at the centre, i.e., at a distance $\left(\frac{L}{2}\right)$ from each rod,
will he

$ B=4 \times \frac{\mu_{0}}{4 \pi} \frac{l}{d}[\sin \alpha+\sin \beta] $
i.e., $B=4 \times \frac{\mu_{0}}{4 \pi} \frac{I}{\left(\frac{L}{2}\right)} \times 2 \sin 45$
i.e., $B_{1} =\frac{\mu_{0}}{4 \pi} \frac{8 \sqrt{2}}{L} I$
So, the flux with smaller loop
$\phi_{2}=B_{1} S_{2}=\frac{\mu_{0}}{4 \pi} \frac{8 \sqrt{2}}{L} l^{2} I$
and hence, $M=\frac{\phi_{2}}{I}=2 \sqrt{2} \frac{\mu_{0}}{\pi} \frac{l^{2}}{L}$
or $M \propto \frac{l^{2}}{L}$