Question

A small block of mass $m$ is fixed at upper end of a massless vertical spring of spring constant $K=\frac{4 m g}{L}$ and natural length $' 10 L^{\prime} .$ The lower end of spring is free and is at a height $L$ from fixed horizontal floor as shown. The spring is initially unstressed and the spring-block system is released from rest in the shown position.

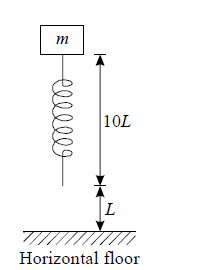
As the block is coming down, the maximum speed attained by the block is:

• A. $\sqrt{g L}$
• B. $\sqrt{3 g L}$
• C. $\frac{3}{2} \sqrt{g L}$
• D. $\sqrt{\frac{3}{2} g L}$

Answer 1

Answer: (C)

At the instant block is in equilibrium position, its speed is
maximum and compression in spring is $x$ given by
$k x=m g$ ......(1)
From conservation of energy
$m g(L+x)=\frac{1}{2} k x^{2}+\frac{1}{2} m v_{\max }^{2}$ .......(2)
from (1) and (2) we get
$v_{\max }=\frac{3}{2} \sqrt{g L}$.