Q.
A sample of 2 kg monoatomic helium (assumed ideal) is taken
through the process ABC and another sample of 2 kg of the
same gas is taken through the process ADC (see fig). Given
molecular mass of helium = 4.
(a) What is the temperature of helium in each of the states
A, B,C and D?
(b) Is there any way of telling afterwards which sample of
helium went through the process ABC and which went
through the process ADC? Write Yes or No.
(c) How much is the heat involved in the process ABC and
ADC?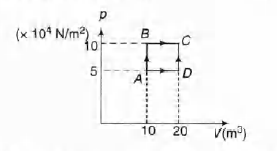
IIT JEEIIT JEE 1997Thermodynamics
Solution: