Q.
A ring of mass $M$ and radius $R$ lies in $x-y$ plane with its centre at origin as shown. The mass distribution of ring is non uniform such that, at any point $P$ on the ring, the mass per unit length is given by $\lambda=\lambda_{0} \cos ^{2} \theta$ (where $\lambda_{0}$ is a positive constant). Then the moment of inertia of the ring about $z$ -axis is: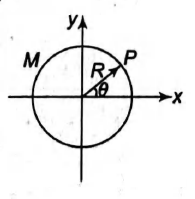
System of Particles and Rotational Motion
Solution: