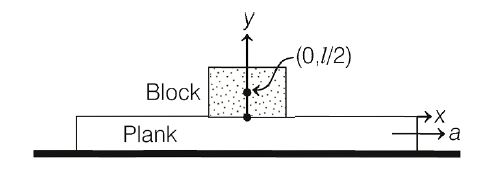
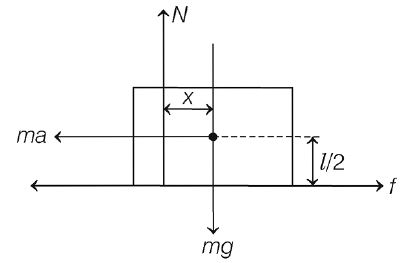
Question

A plank is moving in a horizontal direction with a constant acceleration $a \hat{i}$. $A$ uniform rough cubical block of side $l$ rests on the plank and is at rest relative to the plank

Let the centre of mass of the block be at $(0,l/2) $ at a given instant. If $a = g /10,$ the n the normal reaction exerted by the plank on the block a t that instant acts at

• A. $(0, 0)$
• B. $( - l /2 0 , 0)$
• C. $(- l /10,0)$
• D. $(l /10,0)$

Answer 1

Answer: (B)

Given situation is

Forces acting on the block are

In above diagram,
$ma =$ pseudo force due to acceleration of plank,
$f =$ force of static friction,
$mg =$ weight of block and
$N = $normal reaction.
Here, we must note that due to motion of plank, normal reaction force does not passes through centre of mass.
If line of action of normal force at a distance $x$ from centre, then for equilibrium of block, net torque about centre of mass must be zero.
$\Rightarrow \tau_{\text{Normal reaction }}=\tau_{\text{Friction}}$
$ mg$ and $ma$ does not produces any torque about centre of mass as their line of action passes through centre of mass.
$\Rightarrow N \cdot x=f\cdot l/2$
$\Rightarrow mgx =ma \frac{l}{2}$
$[\because N= mg$ and $f=ma]$
$\Rightarrow x=\left(\frac{a}{g}\right)\frac{l}{2}$
or $x=\frac{1}{10}\cdot\frac{l}{2} \left[\because a=\frac{g}{10}\right]$
or $x=\frac{l}{20} $
So, coordinates of point from which reaction passes are $\left(-\frac{l}{20}\cdot0\right)$