1. Tardigrade
  2. Question
  3. Physics
  4. A person swims in a river aiming to reach exactly on the opposite point on the bank of a river. His speed of swimming is 0.5 m/s at an angle of 120º with the direction of flow of water. The speed of water is

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

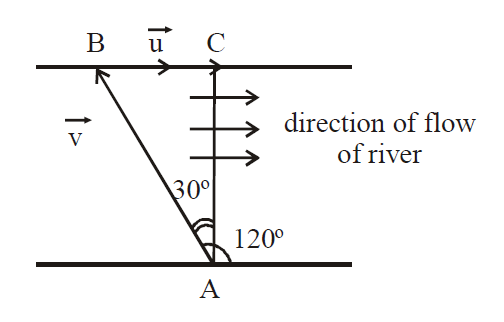
Q. A person swims in a river aiming to reach exactly on the opposite point on the bank of a river. His speed of swimming is $0.5\, m/s$ at an angle of $120^º$ with the direction of flow of water. The speed of water is

VITEEEVITEEE 2019

Solution:

Let the speed of water $=\overrightarrow{u}$
Speed of swimmer $=\overrightarrow{v}=0.5\,m/sec$
Angle between $=\overrightarrow{v}$ and $=\overrightarrow{u}$ is $120^°$. Then
$sin\,\theta=\frac{\vec{u}}{\vec{v}} \Rightarrow \frac{u}{0.5}=\frac{1}{2} or u=0.25\,ms^{-1}$

Solution Image