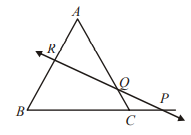
Question

A line $L$ intersects the three sides $B C, C A$ and $A B$ of a $\Delta A B C$ at $P, Q$ and $R$ respectively. Then, $\frac{B P}{P C} \cdot \frac{C Q}{Q A} \cdot \frac{A R}{R B}$ is equal to

• A. 1
• B. 0
• C. -1
• D. None of these

Answer 1

Answer: (C)

Let $A\left(x_{1}, y_{1}\right), B\left(x_{2}, y_{2}\right)$ and $C\left(x_{3}, y_{3}\right)$ be the vertices of $\Delta A B C$ and let $l x+m y+n=0$ be the equation of the line. If $P$ divides $B C$ in the ratio $\lambda: 1$, then the coordinates of $P$ are

$\left(\frac{\lambda x_{3}+x_{2}}{\lambda+1}, \frac{\lambda y_{3}+y_{2}}{\lambda+1}\right)$
Also, as $P$ lies on $L$, we have
$l\left(\frac{\lambda x_{3}+x_{2}}{\lambda+1}\right)+m\left(\frac{\lambda y_{3}+y_{2}}{\lambda+1}\right)+n=0$
$\Rightarrow -\frac{l x_{2}+m y_{2}+n}{l x_{3}+m y_{3}+n}=\lambda=\frac{B P}{P C} \dots$(i)
Similarly, we obtain
$\frac{C Q}{Q A}=-\frac{l x_{3}+m y_{3}+n}{l x_{1}+m y_{1}+n} \dots$(ii)
and $\frac{A R}{R B}=-\frac{l x_{1}+m y_{1}+n}{l x_{2}+m y_{2}+n} \dots$(iii)
On multiplying Eqs. (i), (ii) and (iii), we get
$\frac{B P}{P C} \cdot \frac{C Q}{Q A} \cdot \frac{A R}{R B}=-1$