Q.
A disc of mass $M$ and radius $R$ is rolling with angular speed $\omega$ on a horizontal surface as shown in figure. The magnitude of angular momentum of the disc about the origin $O$ is (here $v$ is the linear velocity of the disc)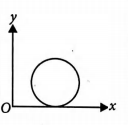
System of Particles and Rotational Motion
Solution: