Q.
A cylinder of cross-sectional area $A$ has two pistons of negligible mass separated by distances $l$ and loaded with spring of negligible mass. An ideal gas at temperature $T_{1}$ is in the cylinder where the springs are relaxed. When the gas is heated by some means its temperature becomes $T_{2}$ and the springs get compressed by $\frac{l}{2}$ each. If $P_{0}$ is the atmospheric pressure and spring constant is $k=\frac{2 P_{0} A}{l}$, then find the ratio of $T_{2}$ and $T_{1} .$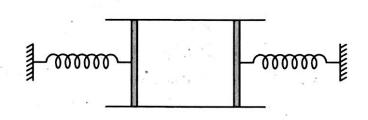
Thermodynamics
Solution: