Question

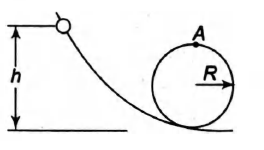
A bead slides without friction around a loop-the-loop (Fig.). The bead is released from rest at a height $h = 3.50R$. How large is the normal force on the bead at point (A) if its mass is 50 g?

• A. 0.10 N downward
• B. 0.10 N upward
• C. 1.0 N downward
• D. 1.0 N upward

Answer 1

Answer: (C)

The speed at the top can be found from the conservation of energy for the bead-track-Earth system,
We define the bottom of the loop as the zero level for the gravitational potential energy.
Since $v_{i}=0, E_{i}=K_{i}+U_{i}=0+m g h=m g(3.50 R)$
The total energy of the bead at point (A) can be written as
$E_{A}=K_{A}+U_{A}=\frac{1}{2} m v_{A}^{2}+m g(2 R)$
Slice mechanical energy is conserved, $E_{i}=E_{A,}$ we get
$m g(3.50 R)=\frac{1}{2} m v_{A}^{2}+m g(2 R)$
simplifying, $v_{A}^{2}=3.0\, g R$
$\Rightarrow v_{A}=\sqrt{3.0\, g R}$
To find the normal force at the top, we construct a force diagram as shown,

Here we assume that $N$ is downward, like mg.
$\Sigma F_{y}=m a_{y}: N+ m g=\frac{m v^{2}}{r}$
$N=m\left[\frac{v^{2}}{R}-g\right]$
$=m\left[\frac{3.0\, g R}{R}-g\right]=2.0\, m g$
$N =2.0\left(50 \times 10^{-3} kg \right)\left(10.0\, m / s ^{2}\right)$
$=1.0\, N$ downward