Q.
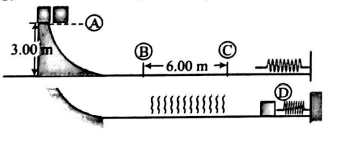
A $10.0- kg$ block is released from rest at point (A) in figure. The track is frictionless except for the portion between points (B) and (C), which has a length of $6.00\, m$. The block travels down the track, hits a spring of force constant $3000 \,N / m$ and compresses the spring $0.20\, m$ from its equilibrium position before coming to rest momentarily. If the coefficient of kinetic friction between the. block and the rough surface between points (B) and (C) is $10\, x$. Find the value of $x$.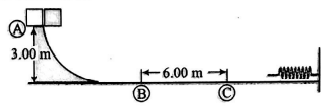
Work, Energy and Power
Solution: