Q.
$0.2$ moles of an ideal gas is taken round the cycle $A B C$ as shown in the figure. The path $B \rightarrow C$ is an adiabatic process, $A \rightarrow B$ is an isochoric process and $C \rightarrow A$ is an isobaric process. The temerature at $A$ and $B$ are $T_{A}=300 K$ and $T_{B}=500 K$ and pressure at $A$ is 1 atm and volume at $A$ is $4.9 L$. The volume at $C$ is
(Given : $\gamma=\frac{Cp}{C_{V}}=\frac{5}{3}, R = 8.205 × 10^{-2}\,L \,atm \,mol^{-1}$
$K^{-1}, \left(\frac{3}{2}\right)^{^{2/5}} =0.81$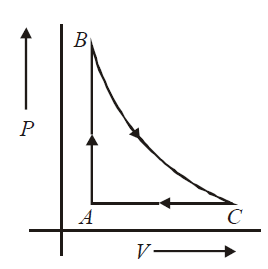
JIPMERJIPMER 2019
Solution: