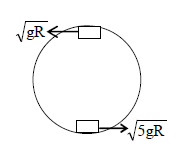
Question

What is the minimum velocity with which a body of mass $m$ must enter a vertical loop of radius $R$ so that it can complete the loop ?

• A. $\sqrt{2gR}$
• B. $\sqrt{3gR}$
• C. $\sqrt{5gR}$
• D. $\sqrt{gR}$

Answer 1

Answer: (C)

To just complete the circle, at the highest point, tension is zero and the gravitational force provides the necessary centripetal force.
Hence, $\frac{m{v}_{top}^2}{R}=mg\dots \dots \dots ...$ (i)
Applying conservation of energy at the top and bottom points,

\frac{1}{2} mv _{\text {bottom }}^{2}= mg \times 2 R +\frac{1}{2} mv _{\text {top }}^{2} \ldots \ldots . . .( ii )

Substituting $m{v}_{\text{top }}^2$ from (i) in (ii) and solving,

v _{\text {bottom }}=\sqrt{5 gR }