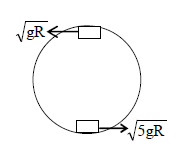
Q. What is the minimum velocity with which a body of mass $m$ must enter a vertical loop of radius $R$ so that it can complete the loop ?
Solution:
To just complete the circle, at the highest point, tension is zero and the gravitational force provides the necessary centripetal force.
Hence, $\frac{ mv _{ top }^{2}}{ R }= mg \ldots \ldots \ldots . . .$ (i)
Applying conservation of energy at the top and bottom points,
$$
\frac{1}{2} mv _{\text {bottom }}^{2}= mg \times 2 R +\frac{1}{2} mv _{\text {top }}^{2} \ldots \ldots . . .( ii )
$$
Substituting $mv _{\text {top }}^{2}$ from (i) in (ii) and solving,
$$
v _{\text {bottom }}=\sqrt{5 gR }
$$