Question

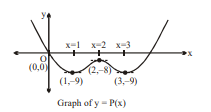
Let $P(x)$ be a polynomial of degree 4 having a relative maximum at $x=2$ and $\underset{x\to 0}{\mathrm{Lim}}\left(3-\frac{P(x)}{x}\right)=27$. Also $P(1)=-9$ and $P^{\prime \prime }(x)$ has a local minimum at $x=2$.
The absolute minimum value of function $y=P^{\prime }(x)$ on the set $A=\left\{x\mid x^2+12\le 7x\right\}$ equals

• A. -1
• B. 0
• C. -9
• D. 3

Answer 1

Answer: (B)

We have
$\underset{x\to 0}{\mathrm{Lim}}\left(3-\frac{P(x)}{x}\right)=27\Rightarrow \underset{x\to 0}{\mathrm{Lim}}\frac{P(x)}{x}=-24$
$\therefore$ Let $P(x)=a{x}^4+b{x}^3+c{x}^2-24x$....(1)
Now, $P(1)=-9\Rightarrow a+b+c=15$....(2)
Also, $P^{\prime }(2)=0\Rightarrow 8a+3b+c=6$....(3)
and $P^{\prime \prime \prime }(2)=0\Rightarrow b=-8a$....(4)
$\therefore$ On solving (2), (3), (4), we get
$a=1,b=-8,c=22$
Hence, $P(x)=x^4-8x^3+22x^2-24x$....(5)

$\therefore P^{\prime }(x)=4x^3-24x^2+44x-24=4\left(x^3-6x^2+11x-6\right)=4(x-1)(x-2)(x-3)$
$\Rightarrow P^{\prime \prime }(x)=4\left(3x^2-12x+11\right)$
Clearly, $P^{\prime \prime }(x)>0\forall x\in [3,4]$ (As $P^{\prime }(x)$ is increasing function on $[3,4]$ )
As $P^{\prime \prime }(x)=4\left(3x^2-12x+11\right)$
So, $P^{\prime \prime }(x)>0\forall x\in [3,4]$
$\Rightarrow P^{\prime }(x)$ is an increasing function on set $A$.
So, $P_{\text{min. }}^{\prime }(x=3)=0$.