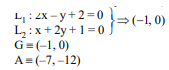- Tardigrade
- Question
- Mathematics
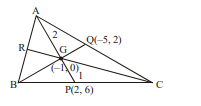
- Let medians L1, L2 and L3 of a triangle A B C belong to the family of lines 2 x-y+2+λ(x+2 y+ 1)=0 where λ is a parameter. Points P, Q, R are the mid-points of sides B C, C A and A B respectively where P ≡(2,6) and Q=(-5,2). If area of triangle B R G is 6 λ where G is centroid of triangle A B C, then find the value of λ.
Q. Let medians and of a belong to the family of lines where is a parameter. Points are the mid-points of sides and respectively where and . If area of is where is centroid of , then find the value of .
Answer: 5
Solution: