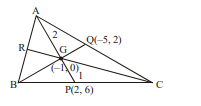
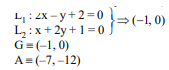Q. Let medians $L_1, L_2$ and $L_3$ of a $\triangle A B C$ belong to the family of lines $2 x-y+2+\lambda(x+2 y+$ $1)=0$ where $\lambda$ is a parameter. Points $P, Q, R$ are the mid-points of sides $B C, C A$ and $A B$ respectively where $P \equiv(2,6)$ and $Q=(-5,2)$. If area of $\triangle B R G$ is $6 \lambda$ where $G$ is centroid of $\triangle A B C$, then find the value of $\lambda$.
Straight Lines
Solution: