Question

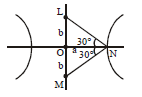
Let $H:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ , where $a>b>0$ be a hyperbola in the $xy$-plane whose conjugate axis $LM$ subtends an angle of $60^{\circ }$ at one of its vertices $N$. Let the area of the triangle $LMN$ be $4\sqrt{3}$

List-I		List-II
P.	The length of the conjugate axis of H is	1.	8
Q.	The eccentricity of H iss	2	$\frac{4}{\sqrt{3}}$
R.	The distance between the foci of H is	3	$\frac{2}{\sqrt{3}}$
S.	The length of the latus rectum of H is	4	4

The correct option is:

• A. P $\to$ 4; Q $\to$ 2; R $\to$ 1; S $\to$ 3
• B. P $\to$ 4; Q $\to$ 3; R $\to$ 1; S $\to$ 2
• C. P $\to$ 4; Q $\to$ 1; R $\to$ 3; S $\to$ 2
• D. P $\to$ 3; Q $\to$ 4; R $\to$ 2; S $\to$ 1

Answer 1

Answer: (B)

$\tan 30^{\circ }=\frac{b}{a}$
$\Rightarrow a=b\sqrt{3}$
Now area of $\Delta LMN=\frac{1}{2}.2b.b\sqrt{3}$
$4\sqrt{3}=\sqrt{3}{b}^2$
$\Rightarrow b=2\&a=2\sqrt{3}$
$\Rightarrow e=\sqrt{1+\frac{b^2}{a^2}}=\frac{2}{\sqrt{3}}$
P. Length of conjugate axis = 2b = 4
So $P\to 4$
Q. Eccentricity $e=\frac{2}{\sqrt{3}}$
So, $Q\to 3$
R. Distance between foci = 2ae
$=2)2\sqrt{3})\left(\frac{2}{\sqrt{3}}\right)=8$
So $R\to 1$
S. Length of latus rectum $=\frac{2b^2}{a}=\frac{2(2{)}^2}{2\sqrt{3}}=\frac{4}{\sqrt{3}}$
So $S\to 2$