Question

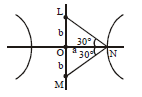
Let $H : \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 $ , where $a > b > 0$ be a hyperbola in the $xy$-plane whose conjugate axis $LM$ subtends an angle of $60^{\circ}$ at one of its vertices $N$. Let the area of the triangle $LMN$ be $4 \sqrt{3}$

List-I		List-II
P.	The length of the conjugate axis of H is	1.	8
Q.	The eccentricity of H iss	2	$\frac{4}{\sqrt{3}}$
R.	The distance between the foci of H is	3	$\frac{2}{\sqrt{3}}$
S.	The length of the latus rectum of H is	4	4

The correct option is:

• A. P $\to$ 4; Q $\to$ 2; R $\to$ 1; S $\to$ 3
• B. P $\to$ 4; Q $\to$ 3; R $\to$ 1; S $\to$ 2
• C. P $\to$ 4; Q $\to$ 1; R $\to$ 3; S $\to$ 2
• D. P $\to$ 3; Q $\to$ 4; R $\to$ 2; S $\to$ 1

Answer 1

Answer: (B)

$\tan30^{\circ} = \frac{b}{a} $
$\Rightarrow a=b \sqrt{3} $
Now area of $\Delta LMN = \frac{1}{2} .2b.b \sqrt{3} $
$4\sqrt{3} = \sqrt{3}b^{2} $
$\Rightarrow b=2 \& a=2 \sqrt{3}$
$ \Rightarrow e = \sqrt{1+ \frac{b^{2}}{a^{2}} } = \frac{2}{\sqrt{3}} $
P. Length of conjugate axis = 2b = 4
So $P \to 4$
Q. Eccentricity $e = \frac{2}{\sqrt{3}}$
So, $Q \to 3$
R. Distance between foci = 2ae
$ = 2 ) 2 \sqrt{3} ) \left( \frac{2}{\sqrt{3}} \right) = 8 $
So $R \to 1$
S. Length of latus rectum $ = \frac{2b^2}{a} = \frac{2(2)^2}{2 \sqrt{3}} = \frac{4}{\sqrt{3}}$
So $S \to 2$