Question

Consider Max. z = - 2x - 3y subject to $\frac{x}{2}+\frac{y}{3}\le 1,\frac{x}{3}\frac{y}{+}2\le 1,x,y\ge 0$ The max value of z is :

• A. 0
• B. 4
• C. 9
• D. 6

Answer 1

Answer: (A)

Given problem is max z = - 2x - 3y
Subject to $\frac{x}{2}+\frac{y}{3}\le 1,\frac{x}{3}+\frac{y}{2}\le 1,x,y\ge 0$
First convert these inequations into equations we get
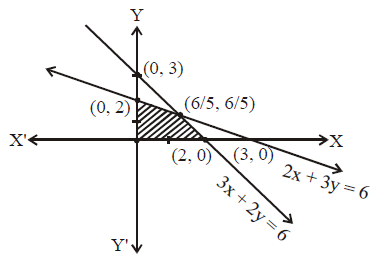
3x + 2y = 6 ...(i)
2x + 3y = 6 ...(ii)
on solving these two equation, we get point of intersection is $(\frac{6}{5},\frac{6}{5})$
Now, we draw the graph of these lines.
Shaded portion shows the feasible region. Now, the corner points are
$(0,2),(2,0),(\frac{6}{5},\frac{6}{5}),(0,0).$
At (0, 2),
value of z = - 2(0) - 3(2) = - 6
At (2, 0),
value of z = - 2(2) - 3(0) = - 4
At $(\frac{6}{5},\frac{6}{5}),(0,0).$
Value of $z=-2\left(\frac{6}{5}\right)-3\left(\frac{6}{5}\right)$
$=\frac{-30}{5}=-6$
At (0, 0), value of z = - 2(0) - 3(0) = 0
At (0, 0), value of z = - 2(0) - 3(0) = 0
$\therefore$ The max value of z is 0.