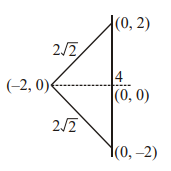Question

Consider a conic $C:y^2=4x$. Let $△PQR$ be an equilateral triangle with side length $k$ where $P$ be any point on $C,Q$ be the foot of perpendicular from $P$ upon the directrix of $C$ and $R$ be the focus of $C$. A circle $C_2$ is inscribed in another conic $C_1:y^2=k(x+1)$ which touches $C_1$ at the points where $C_1$ cuts the $y$-axis. $C_3$ is an ellipse whose auxiliary circle is $C_2$ and major axis coincides with the axis of symmetry of $C_1$ and whose length of minor axis is 4 .
Identify the correct statement(s) for $C_3$.

• A. Eccentricity is $\frac{1}{2}$.
• B. Focal length is 4 .
• C. Length of latus-rectum is $2\sqrt{2}$.
• D. Director circle is $x^2+y^2-4x-8=0$.

Answer 1

Answer: (B), (C), (D)

We have $PM=1+t^2$
$PS=\sqrt{{\left(t^2-1\right)}^2+4t^2}=\left(t^2+1\right)$
$MS=\sqrt{4+4t^2}=2\sqrt{1+t^2}$
$\Rightarrow 2\sqrt{1+t^2}=1+t^2$
$\therefore PM=1+t^2=4=a=k$ (Given)
Hence $C_1:y^2=4(x+1)$
Equation of tangent to $C_1$ at $(0,2)$ is
$2y=4\left(\frac{x+0}{2}+1\right)\Rightarrow y=x+2\text{. }$
Now circle which touches above line at $(0,2)$, is $x^2+(y-2{)}^2+\lambda (x-y+2)=0$
As above circle is passing through the point $(0,-2)$, so
$0+16+\lambda (4)=0\Rightarrow \lambda =-4$
$\therefore C_2:x^2+(y-2{)}^2-4(x-y+2)=0$
$\text{ or }{C}_2:x^2+y^2-4x-4=0$

Now $C_3:\frac{(x-2{)}^2}{a^2}+\frac{y^2}{b^2}=1,a=2\sqrt{2}$ and $b=2$
So $C_3:\frac{(x-2{)}^2}{8}+\frac{y^2}{4}=1$

We have $C_3:\frac{(x-2{)}^2}{8}+\frac{y^2}{4}=1$
(A) $e=\sqrt{1-\frac{4}{8}}=\frac{1}{\sqrt{2}}$
(B) Focal length $=2$ ae $=2\times 2\sqrt{2}\left(\frac{1}{\sqrt{2}}\right)=4$
(C) Latus-rectum $=\frac{2b^2}{a}=2\left(\frac{4}{2\sqrt{2}}\right)=2\sqrt{2}$
(D) Director circle is $(x-2{)}^2+y^2=12\Rightarrow x^2+y^2-4x-8=0$