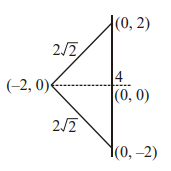Question

Consider a conic $C : y ^2=4 x$. Let $\triangle PQR$ be an equilateral triangle with side length $k$ where $P$ be any point on $C , Q$ be the foot of perpendicular from $P$ upon the directrix of $C$ and $R$ be the focus of $C$. A circle $C _2$ is inscribed in another conic $C _1: y ^2= k ( x +1)$ which touches $C _1$ at the points where $C _1$ cuts the $y$-axis. $C _3$ is an ellipse whose auxiliary circle is $C _2$ and major axis coincides with the axis of symmetry of $C _1$ and whose length of minor axis is 4 .
Identify the correct statement(s) for $C _3$.

• A. Eccentricity is $\frac{1}{2}$.
• B. Focal length is 4 .
• C. Length of latus-rectum is $2 \sqrt{2}$.
• D. Director circle is $x^2+y^2-4 x-8=0$.

Answer 1

Answer: (B), (C), (D)

We have $PM =1+ t ^2$
$PS =\sqrt{\left( t ^2-1\right)^2+4 t ^2}=\left( t ^2+1\right) $
$MS =\sqrt{4+4 t ^2}=2 \sqrt{1+ t ^2} $
$\Rightarrow 2 \sqrt{1+ t ^2}=1+ t ^2$
$\therefore PM =1+ t ^2=4= a = k$ (Given)
Hence $C_1: y^2=4(x+1)$
Equation of tangent to $C_1$ at $(0,2)$ is
$2 y =4\left(\frac{ x +0}{2}+1\right) \Rightarrow y = x +2 \text {. }$
Now circle which touches above line at $(0,2)$, is $x^2+(y-2)^2+\lambda(x-y+2)=0$
As above circle is passing through the point $(0,-2)$, so
$0+16+\lambda(4)=0 \Rightarrow \lambda=-4 $
$\therefore C_2: x^2+(y-2)^2-4(x-y+2)=0$
$\text { or } C_2: x^2+y^2-4 x-4=0$

Now $C _3: \frac{( x -2)^2}{ a ^2}+\frac{ y ^2}{ b ^2}=1, a =2 \sqrt{2}$ and $b =2$
So $C _3: \frac{( x -2)^2}{8}+\frac{ y ^2}{4}=1$

We have $C_3: \frac{(x-2)^2}{8}+\frac{y^2}{4}=1$
(A) $e =\sqrt{1-\frac{4}{8}}=\frac{1}{\sqrt{2}}$
(B) Focal length $=2$ ae $=2 \times 2 \sqrt{2}\left(\frac{1}{\sqrt{2}}\right)=4$
(C) Latus-rectum $=\frac{2 b ^2}{ a }=2\left(\frac{4}{2 \sqrt{2}}\right)=2 \sqrt{2}$
(D) Director circle is $(x-2)^2+y^2=12 \Rightarrow x^2+y^2-4 x-8=0$