- Tardigrade
- Question
- Physics
- A uniform circular disc has radius R and mass m. A particle, also of mass m, is fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. It is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.
Q.
A uniform circular disc has radius R and mass m. A particle, also of mass m, is fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. It is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.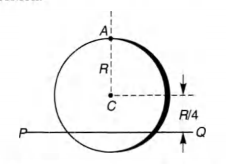
Solution:
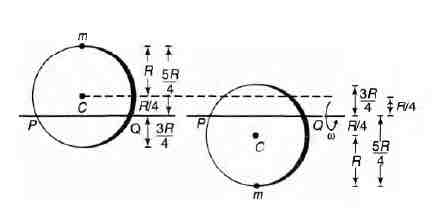
Initial and final positions are shown below. Decrease in potential energy of mass Decrease in potential energy of disc Therefore, total decrease in potential energy of system Gain in kinetic energy of system where I = moment of inertia of system (disc + mass) about axis PQ = moment of inertia of disc + moment of inertia of mass From conservation of mechanical energy, Decrease in potential energy = Gain in kinetic energy Therefore, linear speed of particle at its lowest point