Question

A particle free to move along the x-axis has potential energy given by $U(x)=k[1-exp(-x_2)]for-\infty <x\le +\infty$ , where k
is a positive constant of appropriate dimensions. Then,

• A. at points away from the origin, the particle is in unstable
  equilibrium
• B. for any finite non-zero value of x, there is a force directed
  away from the origin
• C. if its total mechanical energy is $k/2,$ it has its minimum
  kinetic energy at the origin
• D. for small displacements from x = 0, the motion is simple
  harmonic

Answer 1

Answer: (D)

$U(x)=k(1-e^{-x^2})$
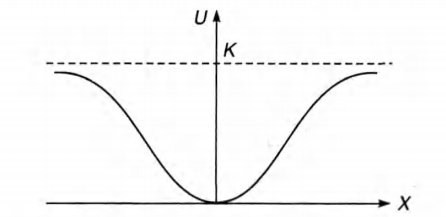
It is an exponentially increasing graph of potential energy
(U) with $x_2.$ Therefore, Uversusx graph will be as shown.
At origin.
Potential energy U is minimum (therefore, kinetic energy
will be maximum) and force acting on the particle is zero
because
$F=\frac{-dU}{dx}=-$ (slope of U -x graph) = 0
Therefore , origin is the stable equilibrium position . Hence
particle will oscillate simple harmonically about x = O for small
displacements. Therefore, correct option is (d).
(a), (b) and (c) options are wrong due to following reasons.
At equilibrium position $F=\frac{-dU}{dx}$= 0 i.e. slope of U-x
graph should be zero and from the graph we can see that
slope is zero at x = 0 and $x=\pm \infty$
Now among these equilibriums stable equilibrium position
is that where U is minimum (Here x = 0). Unstable
equilibrium position is that where U is maximum (Here
none).
Neutral equilibrium position is that where U is constant (Here $x=\pm \infty$ ).
Therefore, option (a) is wrong.
For any finite non-zero value of x, force is directed towards
the origin because origin is in stable equilibrium position.
Therefore, option (b) is incorrect.
At origin, potential energy is minimum, hence kinetic
energy will be maximum. Therefore, option (c) is also
wrong.